脳波解析に使われる「フーリエ変換」

フーリエ変換とは 

「フーリエ変換」を使えば、「連続的なデータを周波数成分に変換」できるため、音声や画像の解析に幅広く使われています。 
脳波のデータも同様に、フーリエ変換を使用することで、効率的に処理できます。 

「重ね合わせ(線形性)」の原理 

例えば「音」は、空気の振動です。この振動を「波形」として表せることは、ご存じかと思います。 
音声信号の「波形」、このような一般に存在するどんな波形も、いくつかの「正弦波の和」に分解できます。これを「重ね合わせの原理」と呼びます。 

正弦波はサイン波ともいい、純粋な単一の周波数を持っている波形です。(例えば、時報の音は「880Hz」という周波数を持っています。) 

この特性を利用して、ある波形がどのような正弦波に分解できるのかを調べることで、 

• ある波形にどんな正弦波が含まれるのか 

つまり 

• ある波形にどんな周波数成分が含まれるのか 

を抽出することができます。 

例えば、このように波形が2つの正弦波に分解できます。 

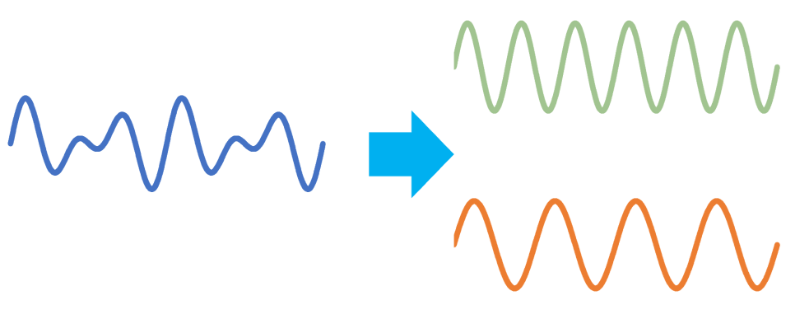 図1: 波形の分解イメージ 

このような単純な例だけでなく、どんな種類の波でも分解する事ができます。その場合、もっと膨大な正弦波の足し算になることがほとんどです。 
では逆に、分解後の正弦波を足し算しなおして、元の波形に近づく様子を見てみましょう。 
もう少し複雑な波形、「ステップ関数」を分解した正弦波を足し算して復元していく様子です。 

 
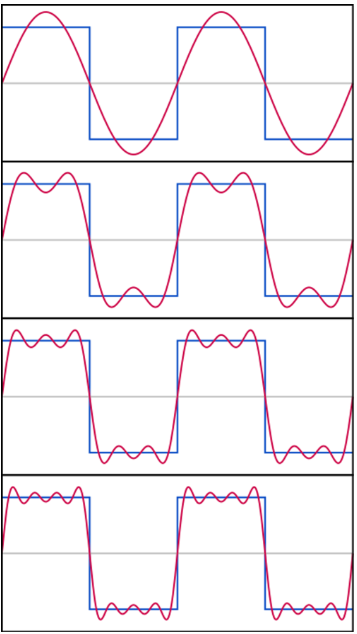
図2: ステップ関数*1分解イメージ図2 
(出典: https://ja.wikipedia.org/wiki/フーリエ級数) 
*1 ステップ関数とは、ある閾値を境にして、入力値が閾値を超えた場合に1を出力し、閾値以下の場合に0を出力する関数です。一般的に、デジタル信号処理や機械学習などの分野で使用されます。 

また、このように波を正弦波に分解する方法は、いつも「ただ1通り」になることがわかっています。  

「直交性」の原理 

波形を表す数式を「関数」として表すことができます。(冒頭で約束したので数式は出しません。) 
それらの「関数」には、”特殊な掛け算ができる”性質があるのですが、この”掛け算”に以下のような特徴があります。 

1. 分解した異なる波長の波を”掛け算”すると0になる 
2. 分解した同じ波長の波を”掛け算”すると、波の大きさに比例した値になる 
3. そしてコンピュータは普通の数字の掛け算と同じように関数の”掛け算”ができる

この2つ目の性質を利用することで、波の各要素、つまり周波数がそれぞれどれくらいの大きさであるかを抽出することができます。そして3つ目の性質、コンピュータで実行すると高速にできるわけです。 

 人間も波の変換を行なっている？？ 

コンピュータは上記の”特殊な関数の掛け算”が得意で、波形を分解・抽出できると書きましたが、実は人間も同様に波を分解しています。 
例えば、私たちは音楽を聴く際に、ギターの音とドラムの音などを聞き分けることができます。これは耳が音を波長ごとに分解するための器官「蝸牛（かぎゅう）」を使い波長などの特徴を聞き分け、波を分解しているからです。 
さらには、音楽だけでなく、私たちは、日常生活の中で常に、話し相手の声を正確に聞き取るために、ノイズを補正しています。これも同じ仕組みであると考えられます。 

脳波との関連性 

脳波は脳神経細胞の活動によって生じる電気的な信号です。脳の活動量や状態によって一般的には以下５つの周波数に分類されます。 
・デルタ波 
・シータ波 
・アルファ波 
・ベータ波 
・ガンマ波 
 
脳波は、異なる周波数に応じた特徴の波が組み合わさって出来ています。 
例えば、睡眠やリラックス効果に密接な関係があり、脳科学や心理学の研究で広く用いられている「アルファ波」は、脳波のうちの8〜13Hzの周波帯にあたります。 
脳波の中でこのアルファ波だけを抽出したい場合、フーリエ変換を使用して脳波から8〜13Hzの周波帯の要素を抽出すれば良いのです。 
機械学習で脳波を分析する場合には、波の周波数や、周波数ごとの強さ、およびその組み合わせを「特徴量」と呼び、さまざまな情報処理を組み合わせて使うことで、脳波を分類できるようになります。 
あらためて、脳波の解析においても、「フーリエ変換」の技術が非常に重要な役割を果たしていることがわかります。 

今回は、脳波の解析手法の１つフーリエ変換をご紹介しました。 
PGVでは、このフーリエ変換も使用して得られた「脳波の特徴量」などを使用して、
脳波AI解析サービス「NAIS Entry」（各ステップでの脳波状態の解析に使用）は実現されています。 
また、PGVのパッチ式脳波計で脳波計測し、計測アプリからデータをPGVのクラウドサービスにアップロードすると、特徴量に変換された脳波データをダウンロードすることが可能です。